A Multi-Layer Solver for XPBD

Abstract: We present a novel multi-layer method for extended position-based dynamics that exploits a sequence of reduced models consisting of rigid and elastic parts to speed up convergence. Taking inspiration from concepts like adaptive rigidification and long-range constraints, we automatically generate different rigid bodies at each layer based on the current strain rate. During the solve, the rigid bodies provide coupling between progressively less distant vertices during layer iterations, and therefore the fully elastic iterations at the final layer start from a lower residual error. Our layered approach likewise helps with the treatment of contact, where the mixed solves of both rigid and elastic in the layers permit fast propagation of impacts. We show several experiments that guide the selection of parameters of the solver, including the number of layers, the iterations per layers, as well as the choice of rigid patterns. Overall, our results show lower compute times for achieving a desired residual reduction across a variety of simulation models and scenarios.
Adaptive Rigidification of Discrete Shells

Abstract: We present a method to improve the computation time of thin shell simulations by using adaptive rigidification to reduce the number of degrees of freedom. Our method uses a discretization independent metric for bending rates, and we derive a membrane strain rate to curvature rate equivalence that permits the use of a common threshold. To improve accuracy, we enhance the elastification oracle by considering both membrane and bending deformation to determine when to rigidify or elastify. Furthermore, we explore different approaches that are compatible with the previous work on adaptive rigidifcation and enhance the accuracy of the elastification on new contacts without increasing the computational overhead. Additionally, we propose a scaling approach that reduces the conditioning issues that arise from mixing rigid and elastic bodies in the same model.
Adaptive Rigidification of Elastic Solids
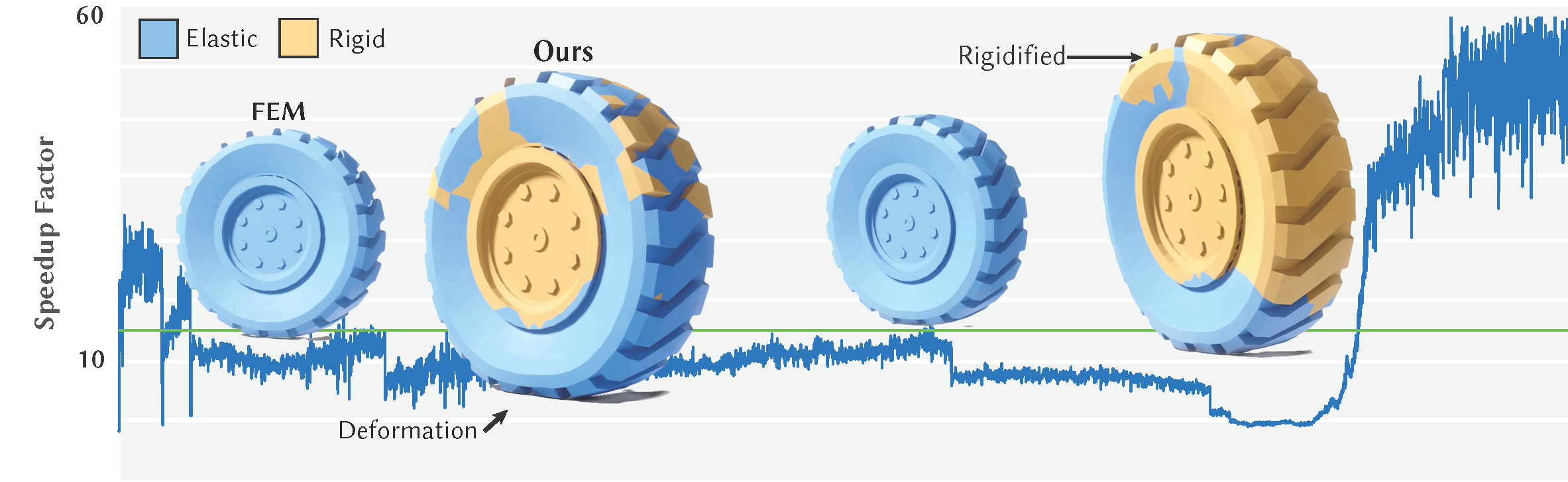
Abstract: We present a method for reducing the computational cost of elastic solid simulation by treating connected sets of non-deforming elements as rigid bodies. Non-deforming elements are identified as those where the strain rate squared Frobenius norm falls below a threshold for several frames. Rigidification uses a breadth first search to identify connected components while avoiding connections that would form hinges between rigid components. Rigid elements become elastic again when their approximate strain velocity rises above a threshold, which is fast to compute using a single iteration of conjugate gradient with a fixed Laplacian-based incomplete Cholesky preconditioner. With rigidification, the system size to solve at each time step can be greatly reduced, and if all elastic element become rigid, it reduces to solving the rigid body system. We demonstrate our results on a variety of 2D and 3D examples, and show that our method is likewise especially beneficial in contact rich examples.
Ordonnancement de tâches sous contraintes sur des métiers à tisser

Abstract: In a textile factory, there are looms. Workers can configure the looms to weave different pieces of textiles. A loom can only weave a piece of textiles if the piece of textiles is compatible with its loom configuration. To change its configuration, a loom requires a setup. The setups are performed manually by workers. There are also sequence-dependent setups to prepare a loom for the upcoming piece of textiles. We wish to minimize the setups duration and the lateness. A solution must satisfy some constraints. The problem is subject to cumulative resources. The quantity of workers simultaneously configuring machines can’t exceed the total number of employees. A loom can only weave a piece of textiles at a time. Scheduling tasks on a single loom is an NP-Hard problem. In this project, we must schedule tasks an average of 800 tasks on 90 looms with a two-week horizon. Stochastic events might occur and must be accounted for. We must design an algorithm to create robust schedules under uncertainty. As a thread breaking during the weaving process isn’t a rare occurrence, a better schedule could greatly impact the performances of a company when applying the schedule to a real situation. We formulate that the number of breaks per task follows a Poisson distribution. First, we propose a branching heuristic based on the traveling salesperson problem in order to leverage computation times. The solutions found are 5 to 30% better according to their objective function than the ones of a greedy heuristic similar to what our industrial partner uses. We also present a filtering algorithm to guarantee robustness of solutions in respect to a confidence level. This algorithm improves robustness and creates more realist schedules. The algorithm is also efficient in computation time by achieving bound consistency in linear time. Combining both these techniques leads to the integration of our research in the decision system of our industrial partner.
The CONFIDENCE Constraint: A Step Towards Stochastic CP Solvers

Abstract: We introduce the CONFIDENCE constraint, a chance constraint that ensures, with probability γ, that a set of variables are no smaller than random variables for which the probability distribution is given. This constraint is useful in stochastic optimization to ensure that a solution is robust to external random events. It allows to control the trade-off between optimizing the objective function and ensuring the satisfiability of the solution under random parameters. We present a filtering algorithm for this constraint with explanations. We apply the constraint to a case study, an industrial scheduling problem where tasks have random processing times due to possible breakdowns during their execution. We evaluate our solutions with simulations and show that this new constraint allows robust solutions in decent computation time.
Leveraging Constraint Scheduling: A Case Study to the Textile Industry

Abstract: Despite the significant progress made in scheduling in the past years, industrial problems with several hundred tasks remain intractable for some variants of the scheduling problems. We present techniques that can be used to leverage the power of constraint programming to solve an industrial problem with 800 non-preemptive tasks, 90 resources, and sequence-dependent setup times. Our method involves solving the traveling salesperson problem (TSP) as a simplification of the scheduling problem and using the simplified solution to guide the branching heuristics. We also explore large neighborhood search. Experiments conducted on a dataset provided by our partner from the textile industry show that we obtain non-optimal but satisfactory solutions.
Multi-Resource Scheduling with Setup Times: An Application Case to the Textile Industry
In the textile industry, the looms are now automatic, but what is left to be automated is the scheduling process. This paper is about the scheduling of the looms and workers doing the setup between two jobs. We explain the problem, tools, methodologies, and constraints to solve this NP-Hard problem. As of now, this is a work in progress.